3 Components of an algorithm: Selection, Sequence, Iteration

3.9.1

  1. It's important to know that similar-looking algorithms have different results because there may be small differences that greatly alter its logic. For example, the usage of a certain mathematical operator rather than another can be enough to produce a completely different return value.
pizzaPrice = 10
money = 9

if pizzaPrice < money:
    print("great! i have more than enough money")
elif pizzaPrice > money:
    print("oh no! i don't have enough money")
else:
    print("phew! i have just enough money")

## TO ##

money = 11

hasEnough = pizzaPrice < money
hasNotEnough = not hasEnough

if hasEnough:
    print("great! i have more than enough money")
elif hasNotEnough:
    print("oh no! i don't have enough money")
else:
    print("phew! i have just enough money")

oh no! i don't have enough money
great! i have more than enough money

3.9.2

Algorithm: make a PB & J sandwich

  1. If hungry, make a sandwich
  2. Find bread. If there is, go to step 4.
  3. If there is no bread, buy bread. Return to step 2.
  4. Find PB & J. If there is, go to step 6.
  5. If there is no PB & J, go to buy PB & J. Return to step 4.
  6. Make sandwich with PB & J and bread.
  7. Eat sandwich. No longer hungry. Return to step 1.
hungry = True
bread = True
pbj = False

def buy_bread():
    global bread
    bread = True
    print("bought bread")

def buy_pbj():
    global pbj
    pbj = True
    print("bought pbj")

def make_sandwich(): 
    global hungry
    hungry = False
    print("yum")

while hungry:
    if bread:
        if pbj:
            make_sandwich()
        else:
            buy_pbj()
    else:
        buy_bread()

bought pbj
yum

3.9.3

Number guesser flowchart: 

import random

#sets variables for the game
num_guesses = 0
user_guess = 0
upper_bound = 100
lower_bound = 0

#generates a random number
number = random.randint(1,100)

# print(number)     #for testing purposes

print(f"I'm thinking of a number between 1 and 100.")

#Write a function that gets a guess from the user using input()
def guess():
    num = input("Guess a number! ")
    return int(num)

#Change the print statements to give feedback on whether the player guessed too high or too low
def search(number, guess):
    global lower_bound, upper_bound
    if guess < number:
        print("Nice try! too low") #change this
        lower_bound = guess
    elif guess > number:
        print("Nice try! too high") #change this
        upper_bound = guess
    return lower_bound, upper_bound

while user_guess != number:
    user_guess = guess()
    num_guesses += 1
    print(f"You guessed {user_guess}.")
    lower_bound, upper_bound = search(number, user_guess)
    print(f"Guess a number between {lower_bound} and {upper_bound}.")

print(f"You guessed the number in {num_guesses} guesses!")

3.11

[12, 14, 43, 57, 79, 80, 99]

  • Middle: 57
  • Second number: 80
  • Tree:

[92, 43, 74, 66, 30, 12, 1]

  • Middle: 66
  • Second number: 74
  • Tree:

[7, 13, 96, 111, 33, 84, 60]

  • Middle: 60
  • Second number: 96
  • Tree:

MC #3: C (not sorted)

import math

def binary_search1(xs, x, start, end):
    if start > end: return -1
    mid = math.floor((start + end) / 2)
    if xs[mid] == x:
        print("x =", x)
        return mid
    if xs[mid] > x:
        print("x <", xs[mid])
        return binary_search1(xs, x, start,  mid-1)
    if xs[mid] < x:
        print("x >", xs[mid])
        return binary_search1(xs, x, mid+1,  end)

def binary_search(xs, x):
    return binary_search1(xs, x, 0, len(xs) - 1)

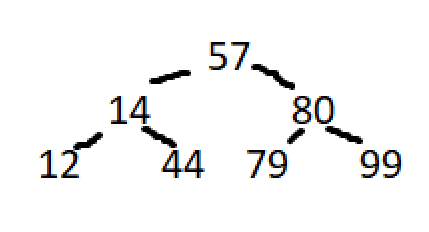
arr1 = [12, 14, 43, 57, 79, 80, 99]
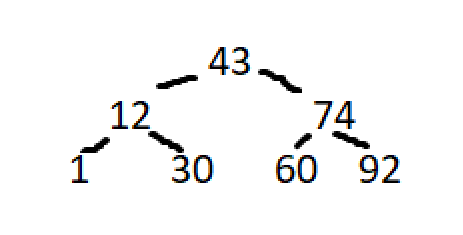
arr2 = [92, 43, 74, 66, 30, 12, 1]
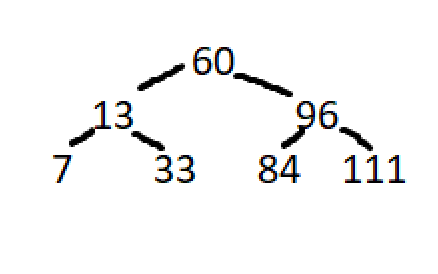
arr3 = [7, 13, 96, 111, 33, 84, 60]

arr2.sort()
arr3.sort()

for (arr, needle) in zip([arr1, arr2, arr3], [14, 12, 84]):
    print("constructing binary search tree:", arr, "searching for", needle)
    print("found {} at idx {}\n".format(needle, binary_search(arr, needle)))

constructing binary search tree: [12, 14, 43, 57, 79, 80, 99] searching for 14
x < 57
x = 14
found 14 at idx 1

constructing binary search tree: [1, 12, 30, 43, 66, 74, 92] searching for 12
x < 43
x = 12
found 12 at idx 1

constructing binary search tree: [7, 13, 33, 60, 84, 96, 111] searching for 84
x > 60
x < 96
x = 84
found 84 at idx 4